24.3.2020

Wir schauen alle seit gut einer Woche gebannt auf die COVID19-Zuwachsraten – gehen diese zurück? Haben die drastischen Maßnahmen, die das Leben in unserem Land und in vielen anderen Ländern derzeit so stark verändern, bereits einen Effekt?

Covid-19 Zuwachsraten: die Ausgangslage

Um wie viel Prozent wir heute mehr oder weniger diagnostizierte Corona-Fälle als noch gestern haben, hängt von vielen Faktoren ab. Von der Ausbreitung der Krankheit, gewiss, aber auch sehr stark davon, wie viel getestet wurde. Können wir für die Anzahl der Tests korrigieren? Wir haben dafür noch keine Möglichkeit gefunden, denn die beiden Größen sind voneinander abhängig: die Anzahl der Tests hängt ja auch davon ab, wie viele Verdachtsfälle getestet werden müssen.

Es gibt aber neben der Testanzahl noch einen anderen Grund für Tagesschwankungen: nicht an jedem Tag der Woche langen gleich viele Testergebnisse ein. Vor allem am Sonntag schienen die Zuwachsraten gering. Hierfür können viele Faktoren ausschlaggebend sein, wie die personelle Besetzung der Labors oder die Informationsweiterleitung der Behörden an Wochenenden.

SORA-Berechnung der Covid-19-Zuwachsraten

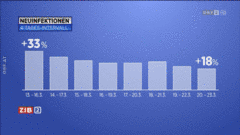
Wir haben uns deswegen vor ein paar Tagen entschieden, die durchschnittlichen Zuwächse über vier Tage zu berechnen (zur Formel weiter unten) und diese zu publizieren. Dies hat den Vorteil, dass das Wochenende immer mit zwei anderen Tagen „im Boot“ ist und so tagestypische Verzerrungen ausgebügelt werden. Darüber hinaus kann jeder Tag auch aus ganz anderen Gründen ein Ausreißer sein, ohne dass dies irgendwas damit zu tun hat, dass es sich um einen Sonntag oder einen Mittwoch handelt.

Die Betrachtung von 4-Tages-Mitteln erspart uns also überflüssige Aufregung über allfällige Ausschläge einzelner Tageszuwächse, in Tagen wie diesen wohl ein berechtigtes Anliegen.

Was wir hier sehen, sind Anzeichen für eine Verlangsamung der relativen Zunahme. Das ist gut so. Wir müssen aber noch so weit kommen, dass diese Zunahme gegen Null geht. Und auf dem Weg dorthin erst einmal – vielleicht auch schon bald – müssen wir es schaffen, dass die absoluten Tages-Zuwächse an Corona-Erkrankungen sich verringern, so weit sind wir auch noch derzeit nicht.

Wichtig: Die Daten bieten einen Blick in die Vergangenheit und keine Zukunftsprognose, was mehrere Gründe hat:

• Positiv getestet werden Menschen, die sich vor einiger Zeit angesteckt haben
• Die Inkubationszeit, die im Schnitt etwas fünf Tage betragen dürfte sowie
• Der zeitliche Abstand zwischen dem Auftreten der ersten Symptome und dem Einlangen des Testresultats.

Unsere Berechnung für die Covid-19-Zuwachsraten bilden daher wahrscheinlich das Krankheitsbild von vor 7 bis 10 Tagen ab.

Was uns die Grafik sagt: Bei allen Unsicherheiten (Abhängigkeit von der Testanzahl, Zufallsschwankungen) kann es sein, dass wir erste Erfolge erzielt haben. Das ist besser, als wenn uns eine Grafik sagen würde, dass wir bislang mit unseren Bemühungen noch nichts ausgerichtet hätten.

Für tägliche Updates und Hintergrundinformationen zu COVID-19 folgen Sie uns auf Twitter.

Anmerkung 29.3.: Der entscheidende Faktor für die Ausbreitung einer Epidemie ist die Reproduktionsrate, d.h. wie viele Personen im Durchschnitt von einer infizierten Person angesteckt werden. Wenn R unter 1 sinkt, gehen die Erkrankungen zurück. In einer Ausbreitungsphase wie der derzeitgen liegt sie über 1, für Österreich gab es dazu Schätzungen der AGES.
Die hier kommunizierten gemittelten relativen Zuwächse sind jedenfalls nicht als Schätzung der Reproduktionsrate oder als Abbildung ihres Verlaufs zu verstehen. Auch aus folgendem Grund: Je länger die Epidemie andauert, enthält die kumulierte Anzahl aller positiven Tests immer mehr Menschen, die inzwischen genesen oder zumindest nicht mehr ansteckend sind. Die kumulierte Zahl aller positiven Tests wächst immer mehr, und sie ist der Nenner in der Formel „Neue Positivtestungen / Summe aller bisherigen Positivtestungen“. Der relative Zuwachs muss daher ab dem Zeitpunkt, an dem es eine substantielle Anzahl genesener Fälle gibt, aus rein mathematischen Gründen sinken.

Die Formel der Berechnung: Die Zahlen in der Grafik sind die Wurzel der 4-Tages-Relation minus 1.  Beispiel:
Am 23.3. um 8 Uhr waren es 3611 Fälle, am 19.3. (8 Uhr) 1843.
(3611/1843)^(1/4) -1= 0,1831 = 18,31% ~ 18%
1843 * 1,1831 * 1,1831 * 1,1831 * 1,1831 ~ 3611.Anders formuliert: Mit der exponentiellen Steigerung können wir feststellen, wie die 4-Tages-Änderung durch eine konstante tägliche Änderung zustande gekommen wäre.